讲解树状数组的实现原理以及使用例子
引入问题
给出一个长度为 $n$ 的数组,完成以下两种操作:
- 将第 $i$ 个数加上 $k$
- 输出区间 $[i,j]$ 内每个数的和
朴素算法
使用树状数组
- 单点修改:$O(\log n)$
- 区间查询:$O(\log n)$
前置知识
lowbit()运算:非负整数 $x$ 在二进制表示下最低位 $1$ 及其后面的 $0$ 构成的数值。
举例说明:
$lowbit(12)=lowbit([1100]_2)=[100]_2=4$
函数实现:
1
2
3
| int lowbit(int x) {
return x & -x;
}
|
树状数组思想
树状数组的本质思想是使用树结构维护前缀和,从而把时间复杂度降为 $O(\log n)$。
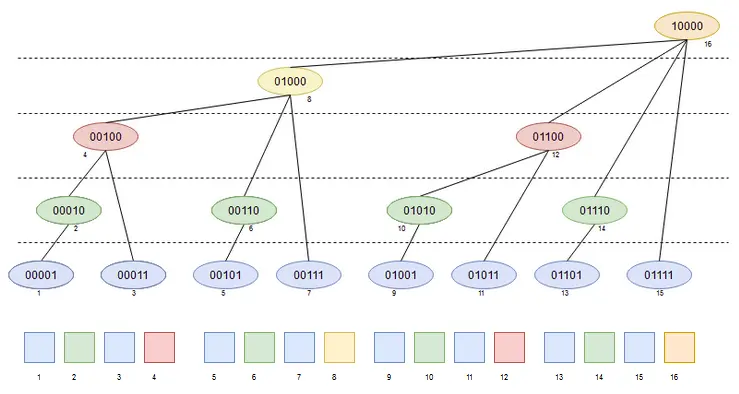
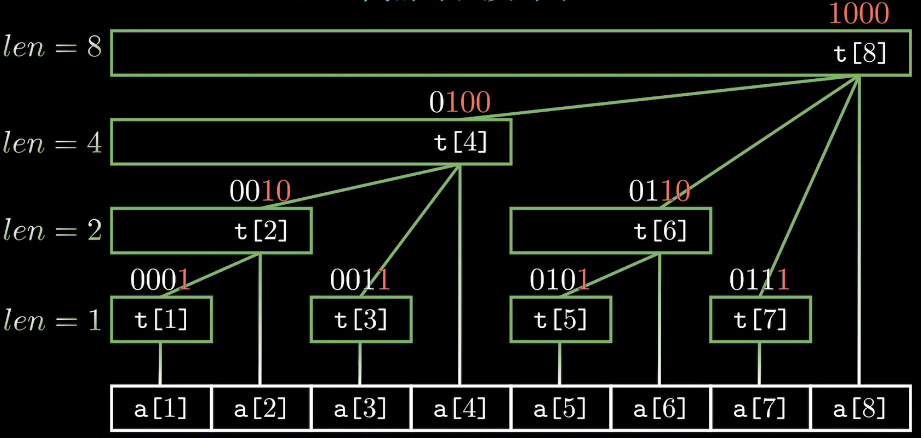
对于一个序列,对其建立如下树形结构:
- 每个结点 $tr[x]$ 保存以 $x$ 为根的子树中叶结点值的和;
- 每个结点覆盖的长度为 $lowbit(x)$;
- $tr[x]$ 结点的父结点为 $tr[x + lowbit(x)]$;
- 树的深度为 $\log_2{n}+1$。
 树状数组
树状数组
树状数组操作
add(x, k)表示将序列中第 x 个数加上 k
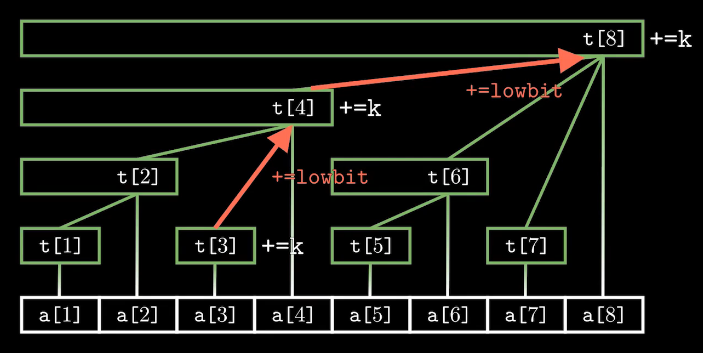
以 add(3, 5) 为例:
在整棵树上维护这个值,需要一层一层向上找到父结点,并将这些结点上的 $tr[x]$ 值都加上 $k$,这样保证计算区间和时的结果正确。时间复杂度为 $O(\log n)$。
 add
add
1
2
3
4
| void add(int x, int k) {
for (int i = x; i <= n; i += lowbit(i))
tr[i] += k;
}
|
sum(x) 表示将查询序列前 x 个数的和
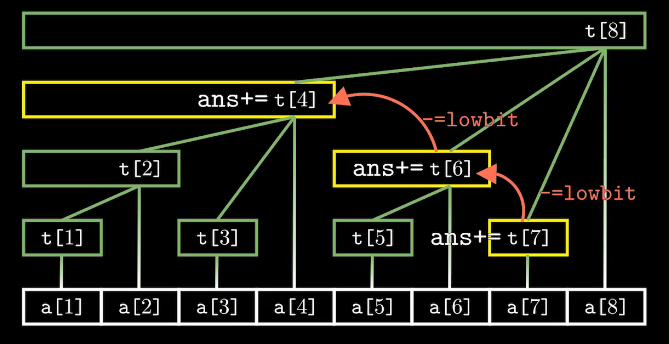
以 sum(7) 为例:
查询这个点的前缀和,需要从这个点向左上找到上一个结点,将加上其结点的值。向左上找到上一个结点,只需要将下标 $x -= lowbit(x)$,例如 $7 - lowbit(7) = 6$。
 sum
sum
1
2
3
4
5
6
| int sum(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i))
res += tr[i];
return res;
}
|
树状数组核心代码
树状数组三大核心操作:
lowbit(x) 求非负整数 $x$ 在二进制表示下最低位 $1$add(x, k) 在第 x 个位置上加上 ksum(x) 求第 1~x 个元素的和
在 c/c++ 中,为了解决一些频繁调用的小函数大量消耗栈空间(栈内存)的问题,特别的引入了 inline 修饰符,表示为内联函数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| inline int lowbit(int x) {
return x & (-x);
}
inline void add(int x, int k) {
for (int i = x; i <= n; i += lowbit(i))
tr[i] += k;
}
inline int sum(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i))
res += tr[i];
return res;
}
|
区间修改,单点查询
- 给区间里的所有数加上 $k$
- 查询某个下标的数的值
差分
先来介绍一下差分
设数组 $a={1,6,8,5,10}$,那么差分数组 $b={1,5,2,-3,5}$
也就是说 $b[i]=a[i]-a[i-1](a[0]=0)$,那么 $a[i]=b[1]+….+b[i]$
假如区间 $[2,4]$ 都加上 $2$ 的话
$a$ 数组变为 $a={1,8,10,7,10}$,$b$ 数组变为 $b={1,7,2,-3,3}$
其中,$b$ 数组只有 $b[2]$ 和 $b[5]$ 变了,因为区间 $[2,4]$ 是同时加上 2 的,所以在区间内 $a[i]-a[i-1]$ 是不变的.
所以对区间 $[x,y]$ 进行修改,只用修改 $b[x]$ 与 $b[y+1]$:
$b[x]=b[x]+k$
$b[y+1]=b[y+1]-k$
因此,本题可以用树状数组维护一个差分序列。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| #include <bits/stdc++.h>
const int N = 500010;
int n, m;
int a[N], tr[N];
inline int lowbit(int x) {
return x & -x;
}
inline void add(int x, int k) {
for (int i = x; i <= n; i += lowbit(i))
tr[i] += k;
}
inline int sum(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i))
res += tr[i];
return res;
}
int main() {
std::ios::sync_with_stdio(0);
std::cin.tie(0);
std::cin >> n >> m;
for (int i = 1; i <= n; i++) {
std::cin >> a[i];
add(i, a[i] - a[i - 1]);
}
int op, x, y, k;
while (m--) {
std::cin >> op;
if (op == 1) {
std::cin >> x >> y >> k;
add(x, k);
add(y + 1, -k);
} else {
std::cin >> x;
std::cout << sum(x) << '\n';
}
}
return 0;
}
|
逆序对
原题链接
逆序对定义:对于给定的一段正整数序列,逆序对就是序列中 $a_i>a_j$ 且 $i<j$ 的有序对。
离散化(Discretization)
在以前介绍的树状数组中,只需要开一个与原序列中最大元素相等的长度数组就行,那么如果我的序列是 1,5,3,8,999,本来 5 个元素,却需要开到 999 这么大,造成了巨大的空间浪费,
离散化就是另开一个数组$d$,$d[i]$用来存放第 $i$ 小的数在原序列的什么位置,比如原序列 $a={999,333,444,21,1}$,第一小就是 1,他在 $a$ 中的位是 5,所以 $d[1]=5$,同理 $d[2]=3$,…,所以 $d$ 数组为 $d={5,3,4,2,1}$,
具体实现:
1
2
3
4
5
6
7
8
9
10
| for (int i = 1; i <= n; i++) {
std::cin >> a[i];
v.push_back(a[i]);
}
std::sort(v.begin(), v.end());
v.erase(unique(v.begin(), v.end()), v.end());
for (int i = 1; i <= n; i++)
a[i] = std::upper_bound(v.begin(), v.end(), a[i]) - v.begin();
|
树状数组求和
根据上面的步骤每一次把一个新的数 x 放进去之后,都要求比他大的元素有几个,而比他大的元素个数一定是 $x+1$ 到 $n$ 中存在数的个数,也就是 $[x+1,n]$ 中有几个数,是不是很耳熟,有点像之前讲的前缀和了,只不过树状数组 $tr$ 表是的不是前缀和了,$tr[x]$ 表示的是 $[1,x]$ 中有几个数已经存在,这样我们每次把一个新的数 $x$ 放进去的时候,都需要把包含这个数的结点更新,然后查询 $[x+1,n]$ 有几个数已经存在。
即 $ans=sum(n)-sum(x)$
具体实现:
1
2
3
4
5
| i64 res = 0;
for (int i = 1; i <= n; i++) {
res += sum(n) - sum(a[i]);
add(a[i], 1);
}
|
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| #include <bits/stdc++.h>
using i64 = long long;
const int N = 500010;
int n;
int w[N], tr[N];
std::vector<int> v;
inline int lowbit(int x) {
return x & -x;
}
inline void add(int x, int k) {
for (int i = x; i <= n; i += lowbit(i))
tr[i] += k;
}
inline int sum(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i))
res += tr[i];
return res;
}
int main() {
std::ios::sync_with_stdio(0);
std::cin.tie(0);
std::cin >> n;
for (int i = 1; i <= n; i++) {
std::cin >> w[i];
v.push_back(w[i]);
}
std::sort(v.begin(), v.end());
v.erase(unique(v.begin(), v.end()), v.end());
for (int i = 1; i <= n; i++)
w[i] = std::upper_bound(v.begin(), v.end(), w[i]) - v.begin();
i64 res = 0;
for (int i = 1; i <= n; i++) {
res += sum(n) - sum(w[i]);
add(w[i], 1);
}
std::cout << res << '\n';
return 0;
}
|